Angelológia dejín z pohľadu vedy 5 (Lineárna regresná metóda – cosinor)

Lineárna regresná metóda je zovšeobecnením Lomb-Scarglovho periodogramu. Na rozdiel od neho ale dokáže nájsť v dátach okrem periodickej zložky aj rôzne trendy. Základný princíp je ale totožný s Lomb-Scarglovým periodogramom. Vstupné dáta sa snažíme aproximovať (lineárnou) kombináciou základných funkcií tak, aby sa minimalizoval súčet štvorcov odchýlok. Rovnako ako Lomb-Scargle aj cosinor je iteratívna metóda. Vychádzame z toho, že dĺžka periódy je neznáma. Aby sme zistili optimálnu dĺžku periódy, musíme vyskúšať rôzne potenciálne dĺžky periód a zvoliť tú, ktorá popisuje naše dáta najlepšie.

Základné funkcie, ktorými sa snažíme aproximovať vstupné dáta, som zvolil nasledovne:
y(t) = 1 – Jednotková funkcia, ktorá má v celom priebehu konštantnú hodnotu 1. Vďaka nej dokážeme pokryť aj dáta s nenulovou strednou hodnotou.
y(t) = t – lineárny trend
y(t) = t² – kvadratický trend

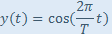
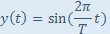
Cosinor je oproti Lomb-Scarglovmu periodogramu presnejší z nasledovných dôvodov:

1. Stredná hodnota je súčasťou lineárneho modelu. Vďaka tomu dokáže cosinor nájsť presnejšiu aproximáciu vstupných dát v prípadoch, keď dĺžka dát nie je celočíselným násobkom hľadaného rytmu. To je napríklad prípad, ak máme historické dáta z 1700 ročného obdobia a hľadáme 500 ročný cyklus. Kým Lomb-Scarglov periodogram strednú hodnotu vždy počíta ako jednoduchý aritmetický priemer vstupných údajov, cosinor prispôsobuje strednú hodnotu hľadanému rytmu tak, aby minimalizoval súčet štvorcov odchýlok. Preto bol aj nájdený nový pojem pre strednú hodnotu dát v cosinor modeli tzv. mesor (z angl. midline estimating statistic of rhytm). Ako rozdiel medzi mesorom a klasickou strednou hodnotou vyzerá v praxi, možno vidieť na nasledovnom obrázku. Vodorovná os znázorňuje dĺžku periódy, zvislá os veľkosť strednej hodnoty vypočítanej pomocou Lomb-Scargle metódy a cosinoru:
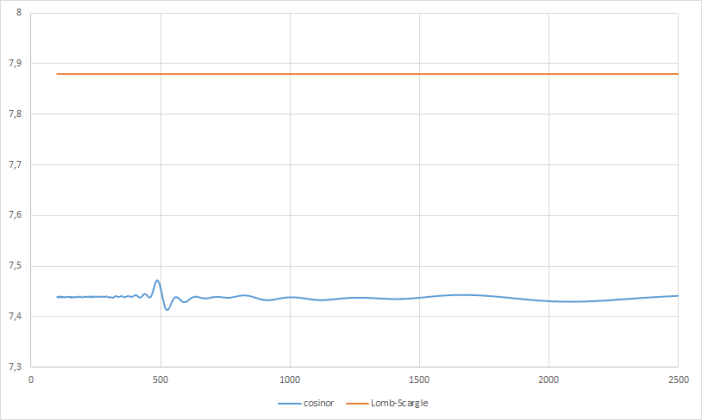   Porovnanie stredných hodnôt vypočítaných pomocou Lomb-Scarglovho periodogramu a cosinoru. Časový priebeh dát, z ktorých boli tieto grafy vypočítané, je možné vidieť na nasledovnom obrázku nižšie.
2. Bežne používané vzorce pre Lomb-Scarglov periodogram obsahujú isté zjednodušenia takže výsledok je len približný. Nepresnosť je ale relatívne malá, takže vo väčšine prípadov ju môžeme zanedbať.

Vďaka vlastnostiam cosinoru dokážeme nájsť periodicitu aj v nasledovných dátach, kde Lomb-Scargle zlyháva na plnej čiare. Modré bodky znázorňujú vstupné dáta, oranžová krivka je optimálna aproximácia:

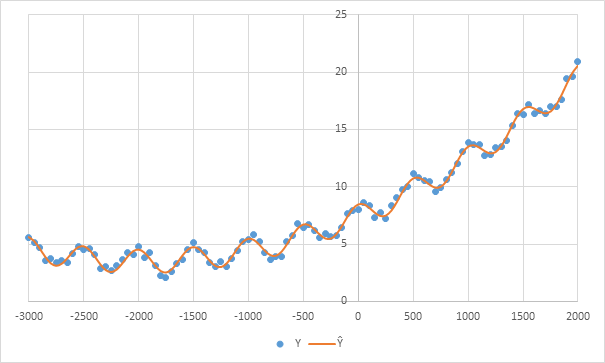
Aproximácia dát lineárnym regresným modelom

Vstupné dáta boli vytvorené simuláciou v Exceli pomocou nasledovného vzorca:
=0,000001*A1*A1+0,004*A1+COS(2*PI()/500*A1)+7+RAND()
Optimálny regresný model podľa výstupu môjho programu je nasledovný:

Ako vidíme program celkom presne odhadol model, pomocou ktorého sa dajú popísať vstupné dáta. Model vysvetľuje až 99,7% variability signálu (zvyšok je šum, ktorý sme do vstupných dát pridali zámerne).

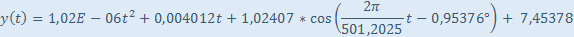
Na vyhodnotenie štatistickej významnosti jednotlivých zložiek lineárneho regresného modelu slúži Fisherov test. Ten nám povie, ktoré zložky modelu sú dostatočne významné na to, aby malo zmysel o nich uvažovať. Pokiaľ napríklad dáta oscilujú plus mínus rovnako hore a dolu okolo strednej hodnoty stane sa nasledovné. Program síce nájde slabý lineárny trend, ale Fisherov test nám povie, že nie je štatisticky významný. Z praktického hľadiska to znamená, že aj keď lineárny trend z modelu vynecháme, nič strašné sa nestane. Inými slovami to znamená, že presnosť modelu sa zníži len zanedbateľne. Toto napr. platí pre priemerné júlové teploty namerané na meteorologickej stanici Hurbanovo v rokoch 1945 – 1975. Tri desaťročia po vojne zostávala klíma konštantná. Otepľovať za začalo až po roku 1975:

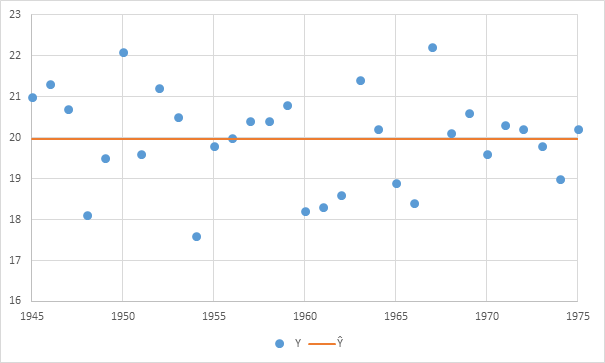
Priemerné júlové teploty (Hurbanovo, 1945 – 1975)

Kvôli overeniu výsledkov som štatistickú významnosť jednotlivých zložiek lineárneho modelu počítal dvoma spôsobmi. Prvý spôsob bol už spomenutý Fisherov test. Druhý spôsob bol tzv. permutačný test založený na Monte Carlo simulácii. Permutačný test simuluje náhodné vplyvy a testuje, v koľkých prípadoch vytvoria periodický signál s rovnakou alebo väčšou amplitúdou, akú sme namerali vo vstupných dátach. Náhodné vplyvy sú simulované pomocou generátora náhodných čísel. Podrobnosti je možné nájsť v odbornej literatúre, ktorú uvádzam na konci článku. Obe metódy dávali prakticky totožné výsledky čo bolo pre mňa uistením, že výpočty mám správne. Správnosť výpočtov som si overil aj v Exceli, nakoľko tento softvér má zabudovaný modul pre výpočet lineárnej regresie. Výsledky sa zhodovali na viac ako 7 platných miest. Výhodou môjho programu oproti Excelu je automatizácia výpočtového procesu vďaka čomu výpočet trvá len niekoľko sekúnd. Excel napríklad nedokáže bez externých skriptov automaticky vypočítať najvhodnejšiu dĺžku periódy. Taktiež nemá zabudovaný permutačný test, ktorým si môžeme overiť vypočítané výsledky aj pre rôzne neštandardné dáta.

Ďalšou nevýhodou Excelu je, že nedokáže vypočítať štatistickú významnosť skupiny regresných koeficientov. To je práve náš prípad, nakoľko nás nezaujíma štatistická významnosť funkcií sin alebo cos osve. My potrebujeme zistiť štatistickú významnosť ich súčtu. Pomer amplitúd sínusovej a kosínusovej zložky lineárneho modelu určuje fázu cyklu. Súčet amplitúd sínusovej a kosínusovej zložky pomocou Pytagorovej vety určuje celkový rozkmit cyklu.

Zoznam použitej literatúry:

1. David G. Kleinbaum, Lawrence L. Kupper, Azhar Nizam, Eli S. Rosenberg: Applied Regression Analysis and Other Multivariable Methods, Brooks Cole, 2013, str. 165 – 214 (popis Fisherovho exaktného testu, t-testu, spôsobu výpočtu parciálnych a viacnásobných parciálnych korelačných koeficientov)
2. Do Q Lee: Numerically efficient methods for solving least squares problems, 2012 (popis numerických metód pre lineárnu regresiu metódou najmenších štvorcov)
3. Marti J. Anderson and John Robinson: Permutation tests for linear models (popis permutačného testu pre regresné koeficienty)
4. William H. Press et al., Numerical Recipes in C, Cambridge University Press, 2002, str. 59 – 70 (popis algoritmu SVD)

Predchádzajúci článok v sérii: Angelológia dejín z pohľadu vedy 4 (Lomb-Scarglov periodogram)

Nasledujúci článok v sérii: Angelológia dejín z pohľadu vedy 6 (Čínski básnici)